يعد علم التفاضل والتكامل من العلوم الأساسية في حياتنا، فبسببه تطور العلم مراحل شاسعة، وتمكن العلماء من القيام بالكثير من الحسابات بدقة كبيرة، فيما كانت سابقاً تكون تقريبيّة.
ما هو التفاضل والتكامل؟
هو أحد الأفرع الرياضيات والذي يهتم بدراسة خواص التوابع العددية مثل النهايات والاستمرار والاشتقاق والتكامل؛ والتي سنتحدث عنها تباعاً. ويأتي الاسم من اللغة اللاتينية (Calculus) والذي يعني حرفياً “الحسبان”.
يمكن القول باختصار أن التفاضل هو إيحاد معدل التغير في التابع (الدالّة)، مثل إيجاد معدل تغير موضع جسم متحرك خلال زمن، والذي يعطينا السرعة. أما التكامل فهو العملية المعاكسة، أي إيجاد التابع من معدّل التغير، مثل حساب مكان جسم عند معرفة تغير موضعه خلال الزمن (السرعة).
لمحة تاريخيّة
الأفكار الأساسية لحساب التفاضل والتكامل موجودة منذ زمن بعد، ابتداءً باليونان القديمة والشرق الأوسط والصين والهند، إلا أن الأسس الرياضياتيّة الواضحة لم توضع حتى القرن السابع عشر على يد السير إسحاق نيوتن، حيث أن إيجاد التفاضل والتكامل لم يكن رفاهية تحتمل الانتظار، بل كان ضرورة لنيوتن ليستخدم هذا العلم في انهاء قوانين الحركة والجاذبية التي وضعها بنفسه.
الأساسيات في حساب التفاضل والتكامل
عند التحدث عن التفاضل والتكامل هناك أساسيات وشروط يجب معرفتها كي تكون الحسابات صحيحة، فكما أن شرط حساب قسمة عددين ألا يكون المقسوم عليه صفراً، هناك قواعد معينة في التفاضل والتكامل، وهذه بعض المفاهيم الأساسية التي يجب معرفتها في هذا العلم.
يجب الإشارة هنا أن الدراسة تكون غالباً على قيم عددية، ويكون التابع معرفّاً على مجال من القيم العددية، وهي القيم التي يتم تعويضها في التابع لحساب ما يسمى المستقر، وهي مجموعة كافة النواتج لكل واحدة من النقاط التي يتم تعويضها في التابع.
- النهايات: تتم دراسة التوابع العددية على مجالات محددة بقيم معينة، أو يمكن ان تكون على مجالات غير محددة، كأن ندرس على مجال يمتد بين اللانهاية الموجبة واللانهاية السالبة مهما كانت حدود المجال فيجب علينا أن نعلم أين تنتهي قيم التابع عند أطراف المجال المدروس، سواءً أكانت قيمة محددة أو قيمة غير محددة (لانهاية).
- الاستمرار: من خلالها يتم دراسة توزع قيم التابع على كل نقطة من مجال التعريف، ويمكننا القول إن التابع مستمر إذا كان الخط الواصل بين جميع نقاط المستقر غير منقطع، بالطبع قد يكون التابع غير مستمر على المجال كلّه، ولكن يكون مستمراً على مجالات جزئيّة فقط منه؛ على سبيل المثال التابع معرفّ بين النقطتين 10 و100، وهو غير مستمر على كافة المجال لكنه مستمر على المجال الجزئي بين 10 و70.
- الاشتقاق: يمكن تعريف المشتق عند نقطة ما ببساطة على أنه المماس للمنحني البياني الذي يمثل التابع أو هو معدل تغير التابع خلال لحظة في غاية الصغر وبصيغة أخرى: هو أصغر تغير يطرأ على التابع خلال أصغر مدة ممكنة.
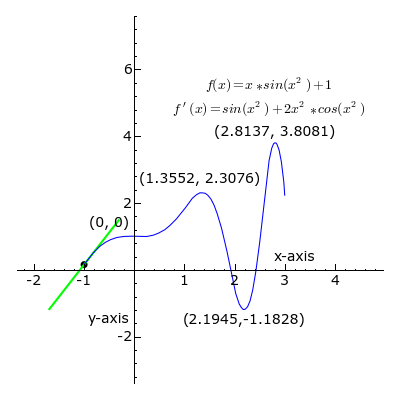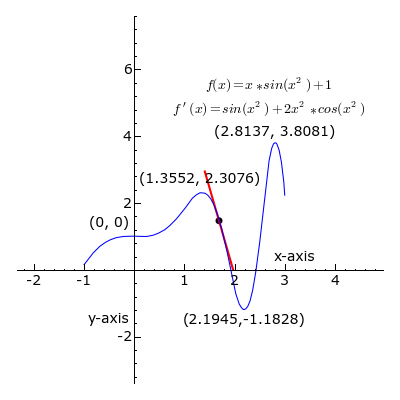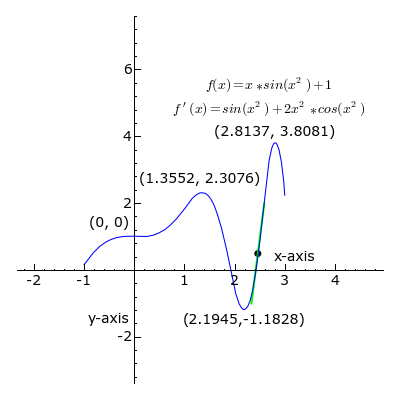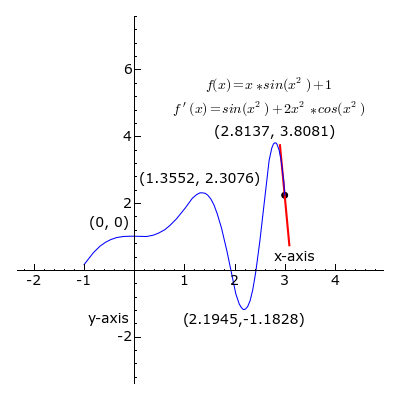
وفي المثال في الصورة أعلاه، مشتق التابع عند كل نقطة، هو ميل المماس لمنحنى لذلك التابع، الخط دائماً مماس للمنحنى الأزرق، وميله يمثل المشتقة. لاحظ يكون المشتق موجب عندما يظهر الخط باللون الأخضر، وسالب عندما يظهر باللون الأحمر، وصفر عندما يظهر الخط باللون الأسود.
يمكن من خلال المشتقات معرفة كيفيّة تغير قيم التابع، والنقاط التي تكون عندها القيمة وعظمى.. الخ
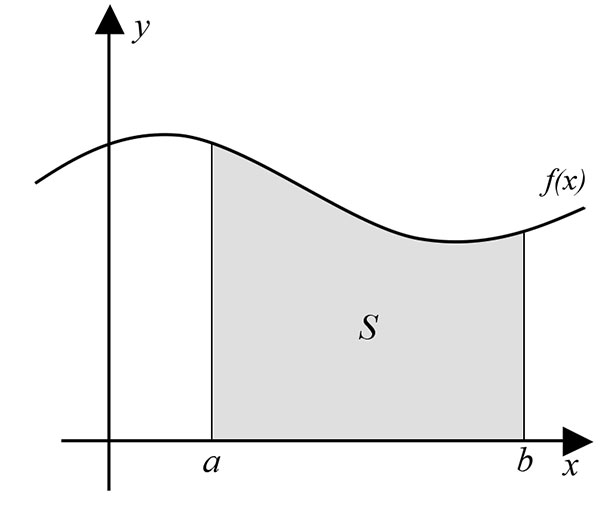
- التكامل: كما ذكرنا فهو العملية العكس للاشتقاق، ويمكن من خلالها حساب المساحات لأشكال غير هندسية مثل منحني ما، أو طول الخط المنحني، أما التعريف الهندسي الدقيق للتكامل: هو المساحة المحضورة بين محور الاحداثيات x والمنحني الخاص بالتابع بين نقطتي مجال التعريف والشكل التالي يوضّح تلك المساحة (S).
التفاضل والتكامل في حياتنا
يعتبر علم التفاضل والتكامل من أهم العلوم لدى الإنسان ومرتبطة بحياته بشكل مباشر مثل الفيزياء والميكانيك والهندسة والاقتصاد والطب وغيرها الكثير، ويمكن القول انه لا يوجد تقريباً علم إلا ويستخدم تطبيقات من التفاضل والتكامل. ومن أهم هذه التطبيقات:
- حساب أطوال المنحنيات، مساحات السطح لأي سطح كان، والحجوم؛ وكل ذلك بدقة كبيرة من خلال تقسيم الشكل لعدد غير منتهي من التغيرات (تغيرات الطول والمساحة والحجم) الصغيرة جداً ومن ثم مكاملتها.
- حساب التوزيعات الاحتمالية المنتظمة، والي يمكن رؤيتها في الفيزياء وحتى في علم الحياء، كحساب انتشار جراثيم في وسط معين تحت ظروف بيئية معينة.
- حل المعادلات التفاضلية وتطبيقاتها مثل النواسات (بيندول) والدارات الكهربائية والحقول الكهرومغناطيسية، حيث يمكن رؤيتها بوضوح في معادلات ماكسويل الأربعة.
- حساب الثوابت في الرياضيات مثل الثابت “باي” (π) أو قيمة العدد النيبري (e) بدقة كبيرة جداً.
- في علم الأدوية يمكن اختبار تأثير دواء ما على عينة جزئية من المرضى ومن ثمّ تعميم نتائج هذه الدراسة على كافة المرضى بمجالات ثقة دقيقة، وذلك من خلال بعض المقاييس الإحصائية الأمر الذي يساعد في اتخاذ القرار بتصنيع هذا الدواء أو إلغائه والبحث عن دواءٍ آخر أكثر فعاليّة.
- في صناعة السيّارات نستطيع عن طريق التكامل أن نحدّد بدقة مركز ثقل السيارة ومحورها المركزيّ ممّا يساعد على تحديد سرعة السيّارة وعوامل الأمان الأخرى.
- أما الهندسة المدنيّة والمعماريّة خاصةً في حساب حجم ومساحات المباني ذات الأشكال الهندسيّة غير المنتظمة الأمر الذي يسهّل للمهندس معرفة ما تطلبه هذه المباني من موادَّ للتصنيع والإكساء فتبدو بغاية الرّوعة والإتقان.
إن أردنا إحصاء المجالات التي يدخل فيها علم التفاضل والتكامل فلن ننتهي بساعات، ولكن يمكن القول أنه السبب في انطلاق الثورة العلمية التي بدورها أدّت للثورة الصناعية والمعلوماتيّة.

